pyblenderSDIC.meshes.create_axisymmetric_mesh#

create_axisymmetric_mesh(profile_curve: ~typing.Callable[[float], float] = <function <lambda>>, frame: ~py3dframe.frame.Frame = Frame(origin=[[0.] [0.] [0.]], x_axis=[[1.] [0.] [0.]], y_axis=[[0.] [1.] [0.]], z_axis=[[0.] [0.] [1.]], height_bounds: tuple[float, float] = (0.0, 1.0), theta_bounds: tuple[float, float] = (0.0, 6.283185307179586), Nheight: int = 10, Ntheta: int = 10, closed: bool = False, first_diagonal: bool = True, direct: bool = True, uv_layout: int = 0) → TriangleMesh3D[source]#

Create a 3D axisymmetric mesh using a given profile curve.

The profile curve is a function that takes a single argument (height) and returns the radius at that height. The returned radius must be strictly positive for all z in the range defined by height_bounds.

The frame parameter defines the orientation and the position of the mesh in 3D space. The axis of symmetry is aligned with the z-axis of the frame, and z=0 corresponds to the origin of the frame. The x-axis of the frame defines the direction of \(\theta=0\), and the y-axis defines the direction of \(\theta=\pi/2\).

The height_bounds parameter defines the vertical extent of the mesh, and theta_bounds defines the angular sweep around the axis. Nheight and Ntheta determine the number of vertices in the height and angular directions, respectively. Nodes are uniformly distributed along both directions.

Note

Nheight and Ntheta refer to the number of vertices, not segments.

For example, the following code generates a mesh of a half-cylinder whose flat face is centered on the world x-axis:

from pyblenderSDIC.meshes import create_axisymmetric_mesh
import numpy as np

cylinder_mesh = create_axisymmetric_mesh(
    profile_curve=lambda z: 1.0,
    height_bounds=(-1.0, 1.0),
    theta_bounds=(-np.pi/4, np.pi/4),
    Nheight=10,
    Ntheta=20,
)

cylinder_mesh.visualize()

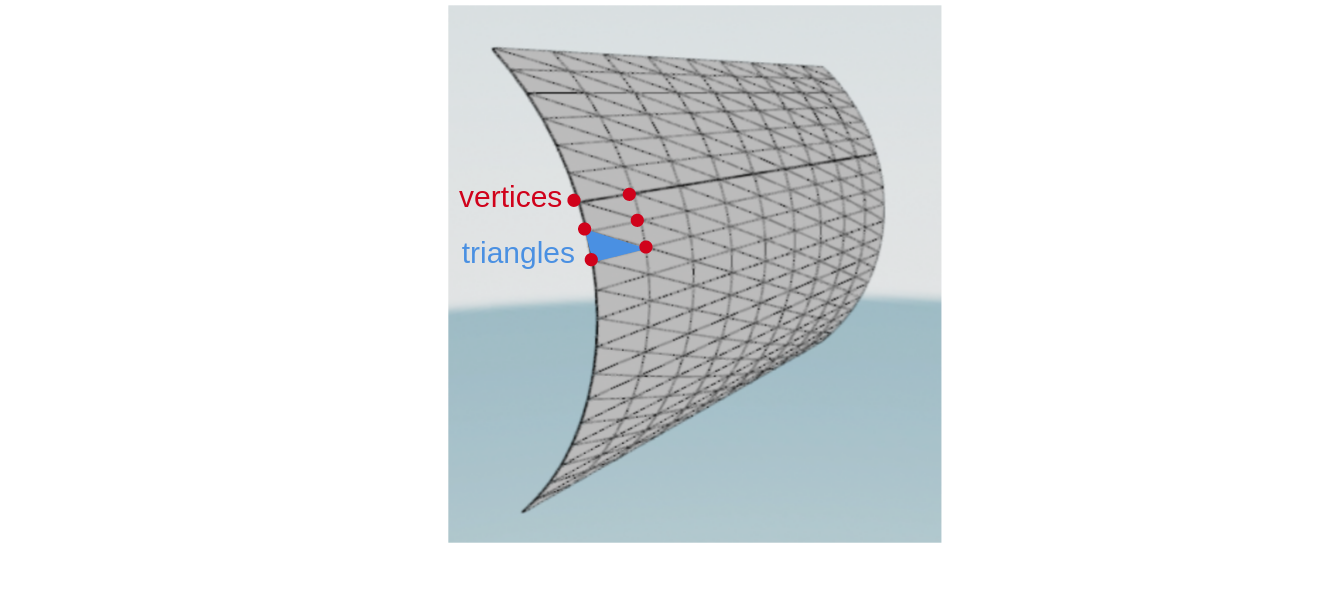
../_images/demi_cylinder_mesh.png — Demi-cylinder mesh with the face centered on the world x-axis.#

Nodes are ordered first in height (indexed by i_H) and then in theta (indexed by i_T). So the vertex at height index i_H and angular index i_T (both starting from 0) is located at:

mesh.vertices[i_T * Nheight + i_H, :]

Each quadrilateral element is defined by the vertices:

\((i_H, i_T)\)
\((i_H + 1, i_T)\)
\((i_H + 1, i_T + 1)\)
\((i_H, i_T + 1)\)

This quadrilateral is then split into two triangles depending on the value of first_diagonal:

If first_diagonal is True:
- Triangle 1: \((i_H, i_T)\), \((i_H, i_T + 1)\), \((i_H + 1, i_T + 1)\)
- Triangle 2: \((i_H, i_T)\), \((i_H + 1, i_T + 1)\), \((i_H + 1, i_T)\)
If first_diagonal is False:
- Triangle 1: \((i_H, i_T)\), \((i_H, i_T + 1)\), \((i_H + 1, i_T)\)
- Triangle 2: \((i_H, i_T + 1)\), \((i_H + 1, i_T + 1)\), \((i_H + 1, i_T)\)

These triangles are oriented in a direct (counterclockwise) order by default (for an observer outside the cylinder). If direct is False, the orientation is reversed by swapping the second and third vertices in each triangle.

If closed is True, the mesh is closed in the angular direction. In that case, theta_bounds should be set to:

\[(\theta_0, \theta_0 \pm 2\pi (1 - \frac{1}{Ntheta}))\]

to avoid duplicating vertices at the seam.

To generate a closed full cylinder:

cylinder_mesh = create_axisymmetric_mesh(
    profile_curve=lambda z: 1.0,
    height_bounds=(-1.0, 1.0),
    theta_bounds=(0.0, 2.0 * np.pi * (1 - 1.0 / 50)),
    Nheight=10,
    Ntheta=50,
    closed=True,
)

The UV coordinates are generated based on the vertex positions in the mesh and uniformly distributed in the range [0, 1] for the OpenGL texture mapping convention. Several UV mapping strategies are available and synthesized in the uv_layout parameter. The following options are available for uv_layout:

uv_layout	Vertex lower-left corner	Vertex upper-left corner	Vertex lower-right corner	Vertex upper-right corner
0	(0, 0)	(Nheight-1, 0)	(0, Ntheta-1)	(Nheight-1, Ntheta-1)
1	(0, 0)	(0, Ntheta-1)	(Nheight-1, 0)	(Nheight-1, Ntheta-1)
2	(Nheight-1, 0)	(0, 0)	(Nheight-1, Ntheta-1)	(0, Ntheta-1)
3	(0, Ntheta-1)	(0, 0)	(Nheight-1, Ntheta-1)	(Nheight-1, 0)
4	(0, Ntheta-1)	(Nheight-1, Ntheta-1)	(0, 0)	(Nheight-1, 0)
5	(Nheight-1, 0)	(Nheight-1, Ntheta-1)	(0, 0)	(0, Ntheta-1)
6	(Nheight-1, Ntheta-1)	(0, Ntheta-1)	(Nheight-1, 0)	(0, 0)
7	(Nheight-1, Ntheta-1)	(Nheight-1, 0)	(0, Ntheta-1)	(0, 0)

The table above gives for the 4 corners of a image the corresponding vertex in the mesh.

pyblenderSDIC.meshes.create_axisymmetric_mesh#

This Page